Hexagonal Grid
Hexagonal grids are used in a variety of strategy games as complicated as Civilization or as simple as Settlers of Catan.
Preamble
In this series we will discuss one way to create a hexagonal grid, create a procedurally generated map, as well as an A* pathfinding algorithm for the end goal of making a simple turn based strategy game centered around WW2.
Introduction
A hexagon is a 6 sided figure comprised of 6 equilateral triangles with angles of 60° . In the image below, the Outer Radius (represented by figure R), is the distance from the center to any corner of the hexagon. The Inner Radius (figure r), is the distance from the center to any side vector. These values allow us to calculate the world position of any given hexagon, and consequently, we can reverse engineer them to get the corresponding hexagon from a world position.
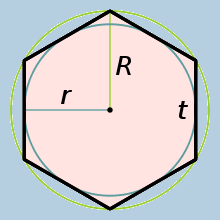
The Inner Radius can be calculated by multiplying the Outer Radius by √3/2. In your GridManager class (or whatever you choose to call it), you should define two public variables for these values. We can calculate the inner radius from the outer, so you can keep that variable hidden.
public float outerRadius; private float innerRadius;
While we're at it, we should also define a Vector2 for the dimensions of the grid. Because we can't have half a hex, we can also make this of type Vector2Int
public Vector2Int gridDimensions;
Like we said previously, we can calculate the inner radius by multiplying the outer radius by √3/2, so we can define that in an Awake() function before we do anything else.
void Awake() { innerRadius = outerRadius * (Mathf.Sqrt(3) / 2); }
To represent an individual hexagon, I am going to define a class named "Node" to house the data. This class will contain information about the hexagon, such as its world position, its terrain type, and whatever else we may need.
For now, I will make sure it's serializable and contains the world position for a hexagon.
[System.Serializable] public class Node() { public Vector2 worldPosition }
Last thing I will do for the setup is create a 1 dimensional array of type Node. This is where I will store all of the grid's data.
[HideInInspector] public Node[] grid;
Grid Generation
Now that we have most of what we need defined, we can move on to actually generating the grid on runtime. For this to work, we need to be able to convert a traditional multi-dimensional array to a single array. The size of the array is very easy to calculate - it's just the grid's x dimension * the grid's y dimension. We can define this in a GenerateGrid() function.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; }
From here, like you would a normal square grid, we have to loop through the grid dimensions to create a Hex for each grid position. You'll notice I'm using z instead of y for our second loop, which is for a reason I'll talk about later.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { } } }
This is good, but how we actually convert a 2d-index (ie take an x value and a y value) to a single index for our array. To accomplish this, we can use the formula below to get our correct position.
array[(X * YGridSize) + Y]
When we add this equation to our existing function, we can correctly index our data within our array.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { grid[(x * gridDimensions.y) + z] = new Node(); } } }
Let's go back to our Node class and define a constructor that requires a world position.
[System.Serializable] public class Node() { public Vector2 worldPosition public Node(Vector2 _position) { worldPosition = _position; } }
Now we can go on to calculate the world position of an individual Hexagon. If you recall from the beginning, we have references to the outerRadius and innerRadius of a Hexagon. To get the correct y position, all we have to do is multiply y with the outer radius and 1.5.
y * outerRadius * 1.5f
Getting the correct x position is trickier. If we just multiply x by 2 * innerRadius, we would get the following effect.
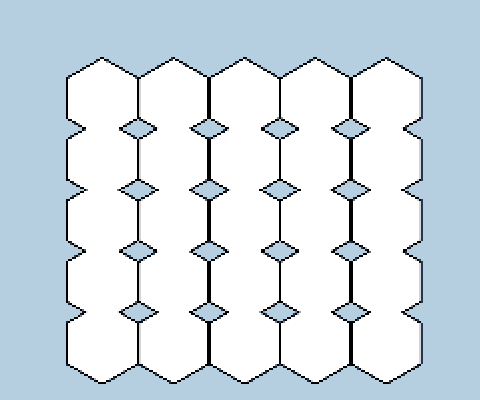
To help fix this, we need to multiply (x + 0.5y) * 2 * innerRadius. However, this only fixes one problem. We want the Hexagons to shift 1 unit left every other iteration.
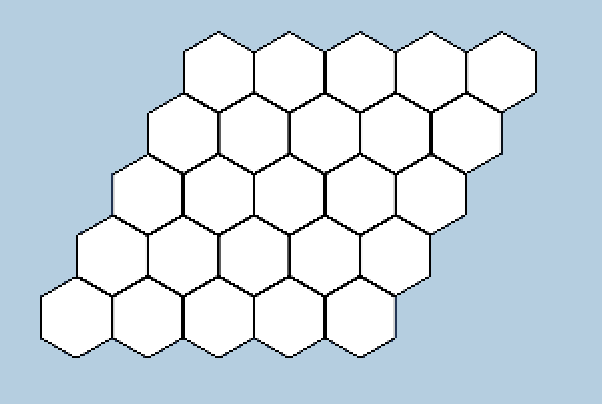
This can be solved by subtracting (x + 0.5y) by y/2, which gives us what we want.
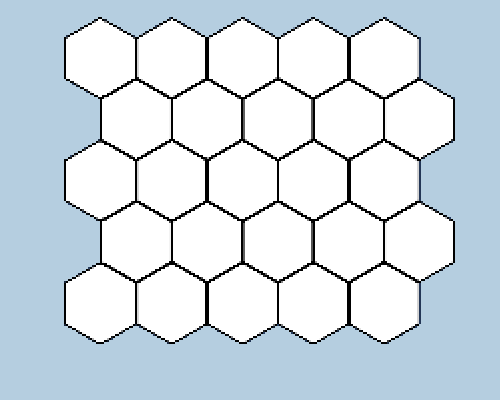
(x + y * 0.5f - y / 2) * (innerRadius * 2)
We can now go back to our GenerateGrid function and add these equations to the loop.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { Vector2 nodePos = Vector2.zero; nodePos.x = (x + y * 0.5f - y / 2) * (innerRadius * 2); nodePos.y = y * outerRadius * 1.5f; grid[(x * gridDimensions.y) + z] = new Node(nodePos); } } }
With this done, we now have to pivot and talk about a concept called the Cube Coordinate System.
Hexagonal Cube Coordinate System
What is the Hexagonal Cube Coordinate System? HCCS is a way to represent any position on a hexagonal grid with a set of 3 (x, y, z) indexes, such that x + y + z = 0. In the image below, the horizontal (green) line represents the z-axis, the red line represents the x-axis, and the purple line of hexagons represents the y-axis.

We can see in the figure below how the values for each axis changes in relation to the distance from each axis. Notice also how any values for any given hexagon will always add up to 0. That means we can determine mathematically the 3rd index if we have the first 2.

To handle this, we can define a new HexCoords class that contains definitions of x, y, and z, as well as a constructor for those values. Like we said, we only need 2 values to find the third, so we only have to define the x and z values in our constructor.
public class HexCoords { public int x; public int z; public int y; public HexCoords(int _x, int _z) { x = _x - _z / 2; z = _z; } }
Two things about this. First, we wont need to update any of the coordinate values once the class is defined, so we can define the set attribute as "private" for x and z.
public class HexCoords { public int x {get; private set; } public int z {get; private set; } public int y; public HexCoords(int _x, int _z) { x = _x - _z / 2; z = _z; } }
Secondly, notice how we didn't define the y value for the coords? we can instead return -x - z whenever the value of y is requested to get the correct index.
public class HexCoords { public int x {get; private set; } public int z {get; private set; } public int y { get { return -x - z; } } public HexCoords(int _x, int _z) { x = _x - _z / 2; z = _z; } }
Obviously, each node has to have a reference to its own coordinates, which we can just define in the Node class. We can also require the input of a HexCoords class into our constructor.
[System.Serializable] public class Node() { public Vector2 worldPosition public HexCoords hexCoords; public Node(Vector2 _position, HexCoords _coords) { worldPosition = _position; hexCoords = _coords; } }
Finally, we just need to pass in a HexCoords class to our nodes when generating the grid to satisfy the constructor.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { Vector2 nodePos = Vector2.zero; nodePos.x = (x + y * 0.5f - y / 2) * (innerRadius * 2); nodePos.y = y * outerRadius * 1.5f; HexCoords hexCoords = new HexCoords(x, z); grid[(x * gridDimensions.y) + z] = new Node(nodePos, hexCoords); } } }
With that done, we can now move on to the final part of this section, actually generating and displaying the grid prefabs.
Displaying your Grid
Now we have all of the backend math done, we can now move to actually display our grid in our game! Displaying your grid is the whole reason you're here, after all . All you need is to define a GameObject prefab and Instantiate() one for every node, then set the GameObject's position to the defined node position we calculated.
Just define a GameObject named hexPrefab or something and create your prefab. Unity has built in geometry for a hexagon, so just modify it to your liking and save it in Assets.
public GameObject hexPrefab;
This is what my prefab looks like (It consists of two hexagons, one black and one white. The white one is slightly smaller than the black one, which gives the effect of a border around it).
Now, in your GenerateGrid() function, Instantiate that prefab for every node. Conveniently, we already have a reference to the hex's world position, so we can just assign the GameObject's transform.position to it.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { Vector2 nodePos = Vector2.zero; nodePos.x = (x + y * 0.5f - y / 2) * (innerRadius * 2); nodePos.y = y * outerRadius * 1.5f; HexCoords hexCoords = new HexCoords(x, z); GameObject newHex = Instantiate(hexagonPrefab); newHex.transform.position = nodePos; grid[(x * gridDimensions.y) + z] = new Node(nodePos, hexCoords); } } }
Now, with the GameObjects being created and displayed, we should now see our grid as so in unity.
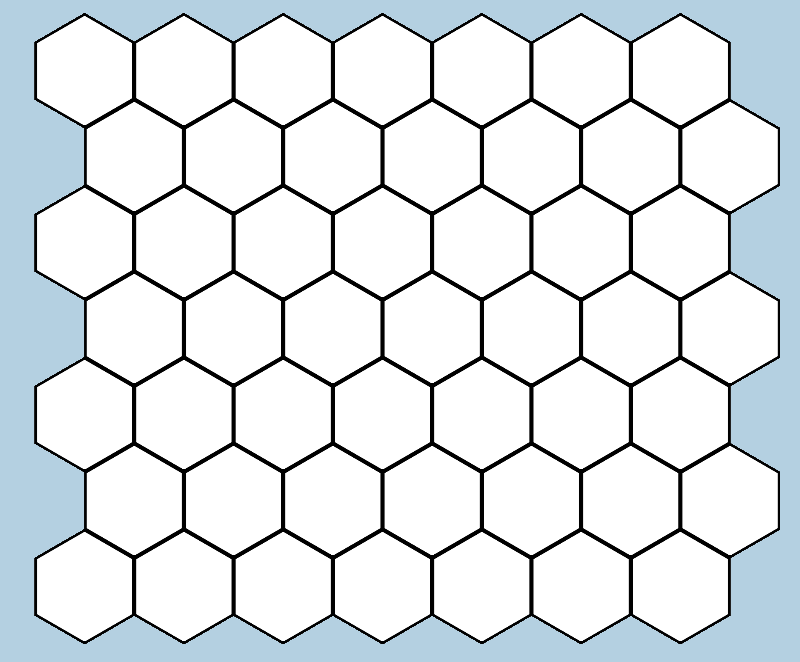
I'm also going to rename each Hex to include its x, y, and z indexes, just for clarity. Also, in the inspector, you will notice that there are hundreds of identical GameObjects clogging up the pipeline, so I'll create a new Parent GameObject to store them.
public void GenerateGrid() { grid = new Node[gridDimensions.x * gridDimensions.y]; GameObject hexParent = new GameObject("Hexagon Holder"); for (int x = 0; x < gridDimensions.x; x++) { for (int z = 0; z < gridDimensions.y; z++) { Vector2 nodePos = Vector2.zero; nodePos.x = (x + y * 0.5f - y / 2) * (innerRadius * 2); nodePos.y = y * outerRadius * 1.5f; HexCoords hexCoords = new HexCoords(x, z); GameObject newHex = Instantiate(hexagonPrefab); newHex.transform.position = nodePos; newHex.transform.parent = hexParent.transform; newHex.name = "Hex X: " + hexCoords.x + " Y: " + hexCoords.y + " Z: " + hexCoords.z; grid[(x * gridDimensions.y) + z] = new Node(nodePos, hexCoords); } } }
With this done, the grid should be displaying correctly on runtime, and is ready to be customized. In the next installment, we will talk about how to set up procedural generation using Perlin noise for the grid.